Barisan aritmatika adalah suatu baris bilangan yang setiap suku berbeda dengan suku sebelumnya dengan jumlah selisih tetap. Sebelum menuju contoh soal barisan aritmatika beserta pembahasannya, silahkan pahami terlebih dahulu konsep dan rumusnya agar kamu bisa lancar mengerjakannya.
Barisan aritmatika sendiri merupakan daftar bilangan yang berurutan dan memiliki selisih tetap. Dari definisi ini, kita dapat menyimpulkan jika bentuk umum dari barisan aritmatika adalah U1, U2, U3, …, U(n+1) atau a, a + b, a + 2b, a + 3b, …, a + (n-1)b.
Kamu masih bingung? Coba perhatikan barisan aritmatika berikut ini.
2, 5, 8, 11, 14, 17, …
Coba kamu bandingkan selisih antara angka pertama dan angka kedua dengan angka kedua dengan angka ketiga. Berapa selisihnya? pasti jawabannya tiga. Nah, selanjutnya coba tebak angka setelah 17 pada barisan tersebut? Pasti jawabannya angka 20.
Maka, dapat disimpulkan jika urutan angka selanjutnya dalam barisan aritmatika merupakan angka sebelumnya ditambah dengan selisihnya.
Namun, bagaimana jika kita disuruh mencari angka ke-puluhan atau ratusan? Tentu jika kita mencarinya manual dengan menjumlahkan angka sebelumnya dengan selisih pasti lama bukan?
Untuk itu, dalam barisan aritmatika, kita dapat menentukan suku ke-n menggunakan rumus umum, yaitu:
Un = a + (n-1)b
Dimana Un adalah suku ke-n, a adalah suku pertama, dan b adalah beda atau selisih.
Untuk menentukan angka selanjutnya dari barisan tersebut, kita harus mencari tahu terlebih dahulu suku pertama dan selisih dari tiap urutan.
Diketahui dari barisan tersebut suku pertama (a) = 2 dan beda (b) = 3.
Selanjutnya, jika kita ingin mengetahui suku ke-7 atau setelah 17 dalam barisan aritmatika tersebut, maka kita dapat menggunakan rumus di atas dan memasukkan nilai suku pertama (a) dan beda (b) yang telah diketahui, sehingga:
U7 = 2 + (7-1)3
U7 = 2 + 17
U7 = 20
Jadi, angka setelah angka 17 dalam barisan aritmatika tersebut adalah angka 20.
Selain itu, kita juga dapat menentukan jumlah n suku pertama dalam barisan aritmatika menggunakan rumus sebagai berikut:

Dimana Sn adalah jumlah n suku pertama, a1 adalah suku pertama, dan d adalah beda atau selisih.
Dalam contoh di atas, misalnya, jika kita ingin mengetahui jumlah 8 suku pertama dari barisan aritmatika tersebut, maka kita dapat menggunakan rumus di atas, sehingga:
Sn = 8/2 (2a + (n-a)b)
S8 = 8/2 (2(2) + (8-1)3)
S8 = 4 (4 + 21)
S8 = 100
Sehingga jumlah 8 suku pertama dari barisan aritmatika tersebut adalah 100.
Catatan: Dari penjelasan konsep dan rumus melalui contoh barisan aritmatika di atas, jangan lupa untuk mengingat rumus-rumusnya. Setidaknya ada 4 rumus dan telah kami rangkum sebagai berikut:
Rumus Barisan Aritmatika
1. Rumus umum untuk mencari suku ke-n pada barisan aritmatika:
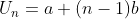
2. Rumus untuk mencari jumlah n suku pertama dari barisan aritmatika:

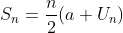
3. Rumus untuk mencari suku pertama pada barisan aritmatika:

4. Rumus untuk mencari beda atau selisih pada barisan aritmatika:

Selanjutnya, untuk membuktikan dan mengukur seberapa jauh pemahamanmu mengenai barisan aritmatika silahkan kerjakan contoh soal barisan aritmatika berserta jawabannya di bawah ini.
Contoh Soal Barisan Aritmatika dan Pembahasannya
Contoh Soal 1
Jika suku pertama dari barisan aritmatika adalah 3 dan beda antar suku adalah 2, maka suku ke-5 adalah?
Pembahasan:
Diketahui:
suku pertama (a) = 3
beda (b) = 2
Ditanyakan: suku ke-5?
Jawab:
Un = a + (n-1)b
U5 = 3 + (5-1)2
= 3 + 8
= 11
Jadi, suku ke-5 dari barisan aritmatika tersebut adalah 11.
Contoh Soal 2
Barisan aritmatika memiliki suku pertama 10 dan suku ke-7 adalah 28. Berapakah beda antar suku pada barisan tersebut?
Pembahasan:
suku pertama (a) = 10
suku ke-7 (U7) = 28
Ditanyakan: beda antar suku?
Jawab:
Un = a + (n – 1)b
U7 = a + (7 – 1)b
28 = 10 + 6b
6b = 18
b = 18/3
b = 3
Atau bisa juga menggunakan cara lain, yaitu sebagai berikut:
b = (Un – a) / (n – 1)
b = (U7 – a) / (7 – 1)
= (28 – 10) / 6
= 18 / 6
= 3
Jadi beda antar suku pada barisan tersebut adalah 3.
Contoh Soal 3
Suku ke-15 dari barisan 70, 61, 52, … adalah …
Pembahasan:
a = 70
b = -9
Un = a + (n-1)b
U15 = 70 + (15-1)-9
= 70 + (-126)
= -56
Dengan demikian, suku ke-15 dari barisan di atas adalah -56.
Contoh Soal 4
Suatu barisan aritmatika mempunyai suku pertama 6 dan suku ke-lima 36, maka jumlah 40 suku yang pertama adalah …
Pembahasan:
Pada soal tersebut diketahui suku pertama (a) = 6, sedangkan untuk beda (b) belum diketahui. Untuk itu kita perlu mencarinya terlebih dahulu dengan menggunakan rumus suku ke-n jika diketahui suku ke-5 adalah 36.
Un = a + (n – 1)b
U5 = 6 + (5 – 1)b
36 = 6 + 4b
4b = 36 – 6
4b = 30
b = 7,5
Terakhir, setelah suku pertama (a) dan beda (b) sudah diketahui maka tinggal memasukkan ke dalam rumus untuk mencari jumlah n suku pertama dari barisan aritmatika.
Sn = n/2 {2a + (n – 1) b}
S40 = 40/2 {2.6 + (40 – 1) 7,5}
S40 = 20 (12 + 39 × 7,5)
S40 = 20 (12 + 292,5)
S40 = 20 (304,5)
S40 = 6090
Jadi, jumlah 40 suku pertama barisan tersebut adalah 6090.
Contoh Soal 5
Rumus suku ke-n dari barisan 5, -2,-9,-16 … adalah …
Pembahasan:
Rumus yang digunakan adalah Un = a + (n-1)b. Karena beda (b) belum diketahui kita harus mencarinya terlebih dahulu
b = U2 – U1
b = -2 – 5
b = -7
Setelah itu, kita hanya perlu memasukkan nilai a dan b kedalam rumus.
Un = a + (n-1)b
Un = 5 + (n-1)-7
Un = 5 + (-7n) + 7
Un = -7n + 12
Dengan demikian, rumus suku ke n dari barisan bilangan di atas adalah -7n + 12.
Contoh Soal 6
Dalam gedung pertunjukkan disusun kursi dengan baris paling depan terdiri dari 12 buah, baris kedua berisi 14 buah, baris ketiga berisi 16 buah, dan seterusnya selalu bertambah 2. Banyaknya kursi pada baris ke-20 adalah …
Pembahasan:
Diketahui:
a = 12
Ditanyakan: banyak kursi pada baris ke-20 (U20)?
Jawab:
Pertama, mencari beda (b) terlebih dahulu agar bisa mencari suku ke-20.
b = U2 – U1
b = 14 – 12
b = 2
Terakhir, mencari suku ke-20.
Un = a + (n – 1)b
U20 = 12 + (20 – 1)2
U20 = 12 + (19)2
U20 = 50
Jadi, banyak kursi pada baris ke-20 adalah 50 buah.
Contoh Soal 7
Diketahui suatu barisan aritmetika dengan suku ke-5 adalah 14 dan suku ke-8 adalah 29.
a. Tentukan suku pertama dan beda barisan tersebut
b. Tentukan suku ke 12 dari barisan tersebut
c. Tuliskan sepuluh suku pertama barisan tersebut
Pembahasan:
Pertama mencari rumus suku ke-n jika diketahui suku ke-5 adalah 14.
Un = a + (n – 1)b
U5 = a + (5 – 1)b
14 = a + 4b
Lalu mencari rumus suku ke-n jika diketahui suku ke-8 adalah 29.
Un = a + (n – 1)b
U8 = a + (8 – 1)b
29 = a + 7b
A. Eliminasikan a untuk mencari b (beda).
a + 7b = 29
a + 4b = 14
____________-
3b = 15
b = 5
Subtitusikan hasil beda (b) ke salah satu persamaan untuk mencari suku pertama (a).
a + 4b = 14
a + 4(5) = 14
a + 20 = 14
a = -6
B. Menentukan suku ke-12
Un = a + (n – 1)b
U12 = -6 + (12 – 1)5
= -6 + (11)5
= -6 + 55
= 49
C. Tuliskan sepuluh suku pertama dari barisan tersebut.
-6, -1, 4, 9, 14, 19, 24, 29, 34, 39
Contoh Soal 8
Suatu barisan 2, 5, 10, 17, … memenuhi pola Un =an2 + bn + c. Suku ke 9 dari barisan itu adalah …
Pembahasan:
Un = an² + bn + c
Un = (1)n2 + 3(0) + 1
Un = n2 + 1
U9 = 92 + 1
U9 = 81 + 1 = 82
Jadi, suku ke-9 pada barisan itu adalah 82.
Contoh Soal 9
Jumlah ke-12 dari barisan 3, 6, 12, 24, … adalah …
Pembahasan:
a = 3
b= 3
Un = a + (n – 1)b
U12 = 3 + (12 – 1)3
U12 = 3 + (11)3
U12 = 3 + 33
U12 = 36
Jadi, jumlah ke-12 dari barisan tersebut adalah 36.
Contoh Soal 10
Beni berhasil lulus ujian saringan masuk PT (perguruan tinggi). Sebagai mahasiswa, mulai bulan 1 agustus 2013, ia menerima uang saku sebesar Rp.15.000.000,00 untuk satu triwulan. Uang saku ini diberikan setiap permulaan triwulan. Untuk setiap triwulan berikutnya uang saku yang diterimanya dinaikkan sebesar Rp.2.500.000,00. Berapa besar uang saku yang akan diterima Beni pada awal tahun 2018 berikutnya?
Pembahasan:
Langkah 1, mencari berapa triwulan Beni menerima uang saku dari bulan Agustus 2013 hingga bulan Januari 2018
Awal terima uang 1/8/2013, karena pada bulan Agustus sudah menerima, maka dihitung mulai bulan Agustus sampai bulan Desember
2013 = 5 bulan
2014 = 12 bulan
2015 = 12 bulan
2016 = 12 bulan
2017 = 12 bulan
2018 = 1 bulan (awal bulan dihitung)
Jumlah semua bulan diatas= 54 bulan
1 triwulan= 3 bulan, maka:
n = 54/3
n = 18 triwulan
Langkah 2, mencari besar uang saku yang akan diterima Beni pada awal tahun 2018
a = 15.000.000
b = 2.500.000
Un = a + (n−1)b
= 15.000.000+(18-1)2.500.000
= 57.500.000
Jadi, besar uang saku yang akan diterima Beni pada awal tahun 2018 adalah Rp.57.500.000,00
Contoh Soal 11
Jika jumlah n suku pertama barisan bilangan: 2, 5, 8, 11, … , 3n – 1 sama dengan 155, maka nilai n adalah …
Pembahasan:
Diketahui:
a = 2
b = 3
Ditanyakan: nilai n?
Jawab:
Sn = n/2 (a + Un)
155 = n/2 (a + Un)
155 . 2 = n (2 + 3n -1)
310 = n (2 + 3n -1)
3n² + n – 310 = 0
(3n + 31)(n -10)=0
n = 10
Jadi nilai n pada barisan bilangan tersebut adalah 10.
Contoh Soal 12
Jika deret suatu barisan aritmatika Sn = 3n2 +1, suku ke delapan suku tersebut adalah …
Pembahasan:
Pertama-tama, kita harus mencari nilai suku pertama (a1) dan beda (d) terlebih dahulu. Caranya dengan mensubtitusikan nilai n = 1 ke dalam persamaan Sn.
Sn =3n2 +1
S1 =3(1)2 +1
a atau U1 = 3 + 1 = 4
Selanjutnya, mencari beda dengan mencari suku kedua lalu dikurangkan dengan suku pertama.
U2 = (3(2)2 +1) – U1
= (3(4) + 1) – 4
= 13 – 4
= 9
Lalu kita mencari beda dengan suku kedua dikurangi suku pertama.
b = U2 – U1
= 9 – 4
= 5
Terakhir, dengan rumus suku ke-n barisan aritmetika akan dicari nilai suku ke-8 seperti berikut:
Un = a + (n-1)b
U8 = 4 + (8-1)5
U8 = 4 + (7)5
U8 = 4 + 35 = 39
Jadi, suku kedelapan adalah 39.






