Pada postingan ini akan membahas contoh soal turunan aturan rantai dan pembahasannya. Namun, sebelum itu alangkah baiknya untuk memahami lebih dahulu materi turunan aturan rantai.
Misalkan y = f(U) dan U = g(x), maka turunan y terhadap x dirumuskan dengan y’ = f'(U) . g'(x). Apabila kamu masih bingung atau ingin memantapkan pemahamanmu, langsung saja perhatikan pada contoh soal turunan aturan rantai berikut ini.
Contoh Soal 1
Turunan pertama dari f(x) = (2x – 5)2 adalah …
Pembahasan:
f(U) = U2
f'(U) = 2U
U = 2x – 5
U’ = 2
f'(x) = f'(U) . U’ = 2U . 2 = 4U
f'(x) = 4(2x – 5)
Contoh Soal 2
Tentukan turunan pertama dari y, jika y = (2x2−4x+1)60
Pembahasan:
f(U) = U60
f'(U) = 60.U60-1 = 60U59
U = 2x2−4x+1
U’ = 2.2x – 4 = 4x – 4
f'(x) = f'(U) . U’ = 60U59 . (4x – 4)
f'(x) = 60(2x2−4x+1)59 (4x – 4)
Contoh Soal 3
Tentukan turunan pertama dari f(x) = (x2 + 4x)3!
Penyelesaian:
f(U) = U3
f'(U) = 3.U3-1 = 3U2
U = x2 + 4x
U’ = 2x + 4
f'(x) = f'(U) . U’ = 3U2 . (2x + 4)
f'(x) = 3(x2 + 4x)2 (2x + 4)
Contoh Soal 4
Turunan dari f(x) = 5 (x2 + 2x – 1)3 adalah …
Penyelesaian:
f(U) = 5U3
f'(U) = 15U2
U = x2 + 2x – 1
U’ = 2x + 2
f'(x) = f'(U) . U’
f'(x) = 15U2 . (2x + 2)
f'(x) = 15 (x2 + 2x – 1)2 . (2x + 2)
f'(x) = 30 (x + 1) (x2 + 2x – 1)2
Contoh Soal 5
Jika \( f(x) = \sqrt{6x + 7} \), maka nilai \( f'(3) = \) …
a. 2/3
b. 3/5
c. 5/7
d. 7/9
Pembahasan:
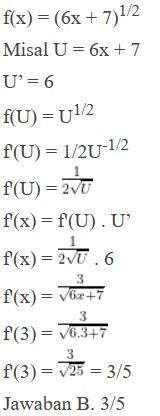
Contoh Soal 6
Jika y = (x2 − 3)5 dan y’ adalah turunan pertama y, maka tentukanlah nilai dari y'(2).
Pembahasan:
f(U) = U5
f'(U) = 5.U5-1 = 5U4
U = x2 − 3
U’ = 2x
f'(x) = 5U4 . 2x = 10x . U4
f'(x) = 10x (x2 − 3)4
f'(2) = 10 . 2 (22 – 3)4 = 20 (1)4 = 20
Contoh Soal 7
Tentukan turunan pertama untuk setiap fungsi yang berikut.
a. \( f(x) = \sqrt{1 + 4x^2} \)
b. \( f(t) = \sqrt{1 – 3t^2} \)
Pembahasan:
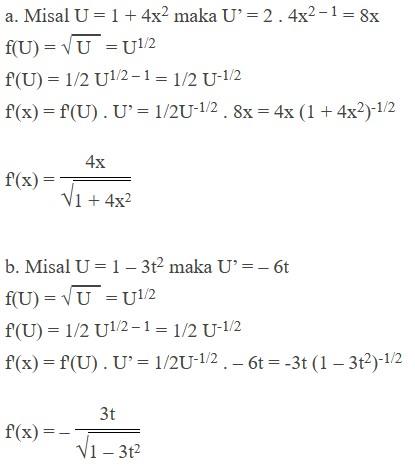
Contoh Soal 8
Diketahui \( f(x) = \frac{x^2 + 3}{2x + 1} \). Jika \( f(x) \) menyatakan turunan pertama \( f(x) \), maka \( f(0) + 2f'(0) \) adalah …
a. -10
b. -9
c. -7
d. -5
Pembahasan

Contoh Soal 9
Jika \(y’\) merupakan turunan pertama dari \(y = \sqrt[3]{6x^2 + 3}\), maka tentukan nilai \(y'(2)\)!
Pembahasan:
y = (6x2 + 3)1/3
f(U) = U1/3
f'(U) = 1/3 . U1/3 – 1 = 1/3 U-2/3
U = 6x2 + 3
U’ = 2.6x = 12x
y’ = 1/3 U-2/3 . 12x
= 4x (6x2 + 3)-2/3
y'(2) = 4(2) . (6 (2)2 + 3)-2/3
y'(2) = 8 (27)-⅔

Contoh Soal 10
Tentukan turunan pertama dari fungsi di bawah ini.
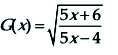
Pembahasan:

Contoh Soal 11
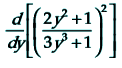
Turunan pertama dari fungsi di samping adalah …
Pembahasan:







